布尔索引

阅读: 5415 评论：2

Numpy给我们带来的最神奇的操作其实是布尔数组索引方法。

使用布尔数组进行索引，其实就是我们显式地选择数组中需要哪些项，不需要哪些项。

最自然的方法是使用与原始数组形状相同的布尔数组进行筛选过滤：

>>> a = np.arange(12).reshape(3,4)
>>> b = a > 4
>>> b   # 通过比较运算，b变成了一个由布尔值组成的数组
array([[False, False, False, False],
       [False,  True,  True,  True],
       [ True,  True,  True,  True]])
>>> a[b]        # 生成一个由True值对应出来的一维数组
array([ 5,  6,  7,  8,  9, 10, 11])

这个技巧用在特殊位置赋值操作特别高效：

>>> a[b] = 0    #所有a中大于4的元素被重新赋值为0
>>> a
array([[0, 1, 2, 3],
       [4, 0, 0, 0],
       [0, 0, 0, 0]])

实际上，上面的操作可以简写成：a[a>4] = 0

使用~可以对布尔值取反，|表示或，&表示与：

>>> a[~b]
array([0, 1, 2, 3, 4])
>>> (a<4)|(a>7)
array([[ True,  True,  True,  True],
       [False, False, False, False],
       [ True,  True,  True,  True]])
>>> a[(a<4)|(a>7)]
array([ 0,  1,  2,  3,  8,  9, 10, 11])
>>> (a>3)&(a<8)
array([4, 5, 6, 7])

下面是一个复杂的实际例子，它使用布尔数组对原始数组进行索引，最终生成了曼德勃罗特函数，并通过matplotlib将它绘制出来：

>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> def mandelbrot( h,w, maxit=20 ):
...     """Returns an image of the Mandelbrot fractal of size (h,w)."""
...     y,x = np.ogrid[ -1.4:1.4:h*1j, -2:0.8:w*1j ]
...     c = x+y*1j
...     z = c
...     divtime = maxit + np.zeros(z.shape, dtype=int)
...
...     for i in range(maxit):
...         z = z**2 + c
...         diverge = z*np.conj(z) > 2**2     # 生成布尔数组
...         div_now = diverge & (divtime==maxit)  # 进一步处理
...         divtime[div_now] = i                  # 进行索引
...         z[diverge] = 2                        # 避免多次操作
...
...     return divtime
>>> plt.imshow(mandelbrot(400,400))
>>> plt.show()

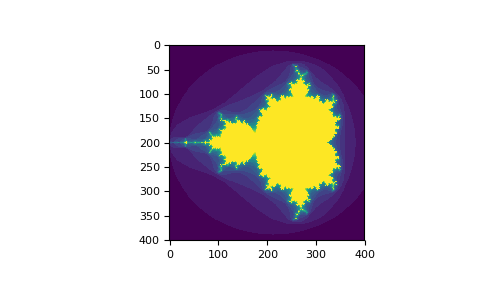
注：曼德勃罗特集是人类有史以来做出的最奇异,最瑰丽的几何图形，曾被称为“上帝的指纹”。这个点集均出自公式:Zn+1=(Zn)^2+C。这是一个迭代公式,式中的变量都是复数。这是一个大千世界,从他出发可以产生无穷无尽美丽图案，他是曼德勃罗特教授在二十世纪七十年代发现的。

另一种使用布尔数组索引的方法，就是类似前面小节中介绍的方法:

>>> a = np.arange(12).reshape(3,4)
>>> b1 = np.array([False,True,True])             
>>> b2 = np.array([True,False,True,False])      
>>>
>>> a[b1,:]                                 
array([[ 4,  5,  6,  7],
       [ 8,  9, 10, 11]])
>>>
>>> a[b1]                                     
array([[ 4,  5,  6,  7],
       [ 8,  9, 10, 11]])
>>>
>>> a[:,b2]                                  
array([[ 0,  2],
       [ 4,  6],
       [ 8, 10]])
>>>
>>> a[b1,b2]                                  
array([ 4, 10])

补充解释一下上面最后的例子：

>>> a = np.arange(12).reshape(3,4)
>>> b1 = np.array([True,False,True])

>>> b1.nonzero()   # 调用nonzero方法，就相当于将值为True的下标索引拿出来，保存到一个新数组中
(array([0, 2], dtype=int64),)

>>> a[b1]
array([[ 0,  1,  2,  3],
       [ 8,  9, 10, 11]])

>>> a[b1.nonzero()]             #可以看到，布尔数组索引等同于它的nonzero()数组索引的结果
array([[ 0,  1,  2,  3],
       [ 8,  9, 10, 11]])

>>> b2 = np.array([True,False,True,False])

>>> b2.nonzero()
(array([0, 2], dtype=int64),)

>>> a[b2.nonzero()]
array([[ 0,  1,  2,  3],
       [ 8,  9, 10, 11]])

>>> a[b1,b2]    
array([ 0, 10])

>>> a[b1.nonzero(), b2.nonzero()]       # 同时使用两个布尔数组进行索引， 相当于用它们的nonzero()进行索引
array([[ 0, 10]])       # 也就是获取a[0][0],a[2][2]。理解这点很重要！这时候从按行列索引，变成了按下标组合的索引方式。



# 要注意的是使用这种方法，b1和b2布尔数组的长度，必须相等或者可以广播。注意，这个广播机制很重要！
>>> b2 = np.array([True,False,True,True])

>>> b2.nonzero()
(array([0, 2, 3], dtype=int64),)

>>> a[b1, b2]
IndexError                                Traceback (most recent call last)
<ipython-input-26-c7d1e0872c96> in <module>
----> 1 a[b1, b2]

IndexError: shape mismatch: indexing arrays could not be broadcast together with shapes (2,) (3,) 
#上面，长度2和长度3的两个索引数组无法广播，所以会出错。而下面长度1和2的两个数组，长度为1的可以广播，因此不会报错。


>>> b2 = np.array([False,False,True,False])

>>> b2.nonzero()
(array([2], dtype=int64),)
>>> a[b1,b2]
array([ 2, 10])

花式索引统计方法

评论总数： 2

点击登录后方可评论

>>> a[b1,b2] array([ 4, 10]) 这一步怎么来的？？求告知

By 汪森14049 On 2019年7月10日 17:09 回复

当使用a[b1,b2] 这种方式的时候，布尔数组可以看作对应的nonzero()数组索引的结果。并且这时候由整行整列索引，变成了由下标组合一个一个元素索引的方式了。具体参考我补充的例子。

博主回复汪森14049 2019年7月10日 20:13 回复